Types of Distance Measures
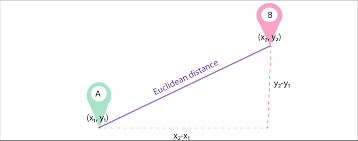
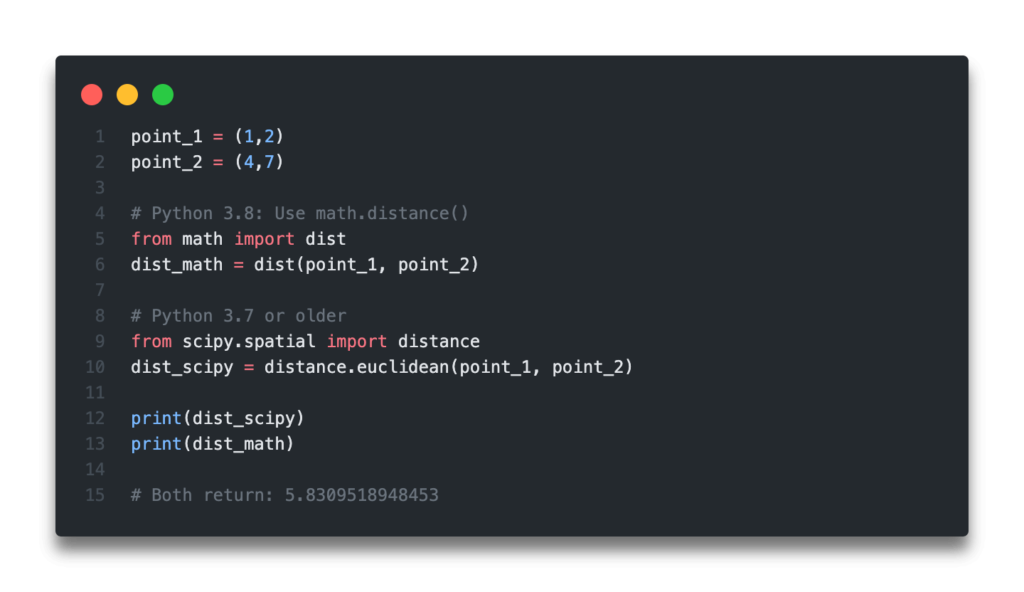
Euclidean Distance
Euclidean Distance is one of the most commonly used distance metrics. Mathematically it is the square root of the sum of differences between two different data points.
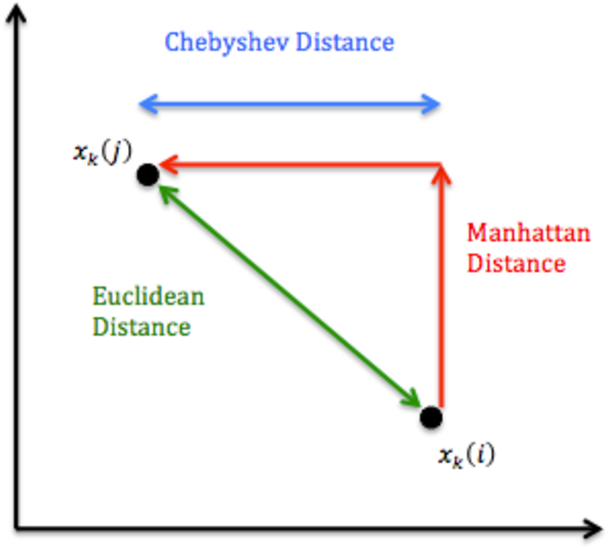
Manhattan Distance (L1 Distance or Cityblock Distance)
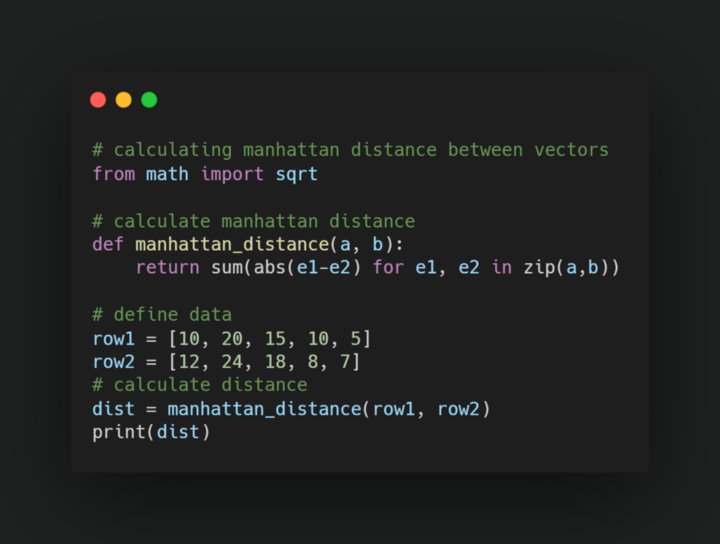
Manhattan Distance calculates the distance between two real-valued vectors. Mathematically Manhattan distance is calculated as the sum of absolute distances between two different data points.
Mostly it is recommended to use Manhattan distance instead of Euclidean distance when we have real value vectors in integer dimensional space.
Chebyshev Distance (Chessboard Distance)
The Chebyshev distance is calculated as the maximum of the absolute difference between two different vectors.
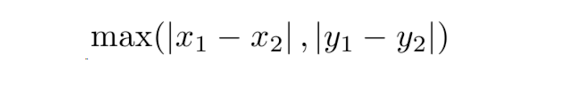
An intuitive example of Chebyshev distance is a drone that has two independent motors: one motor to go forward and one motor to go sideways. Both motors can run at the same time and they can both be at maximum speed at the same time.
It is widely used in Computer-Aided Manufacturing applications for the optimization of machines operating in planes.
Hamming Distance
Hamming Distance measures the similarity between two string which must be of the same length. Hamming Distance basically quantifies if two attributes are different or not. When they are equal Hamming distance is 0 else 1.
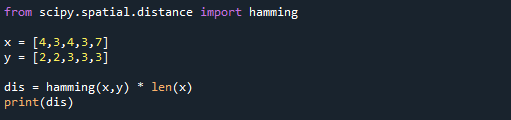
Hamming Distance is used when we have categorical attributes in our data.
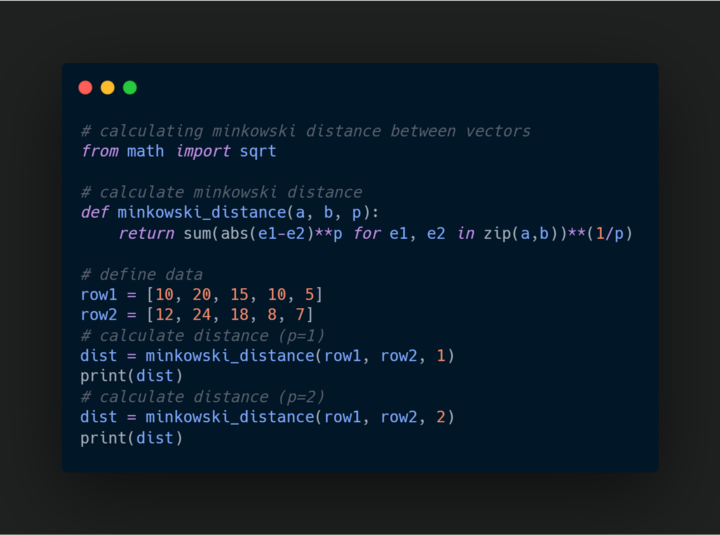
Minkowski Distance
Minkowski Distance generalizes Euclidean and Manhattan Distance.. It is widely used in the field of Machine learning, especially in the concept to find the optimal correlation or classification of data. Minkowski distance is used in certain algorithms also like K-Nearest Neighbors, Learning Vector Quantization (LVQ), Self-Organizing Map (SOM), and K-Means Clustering.
Cosine Distance
Cosine similarity basically measures the similarity between two non-zero vectors. It is basically the cosine angle between two vectors that are most similar.
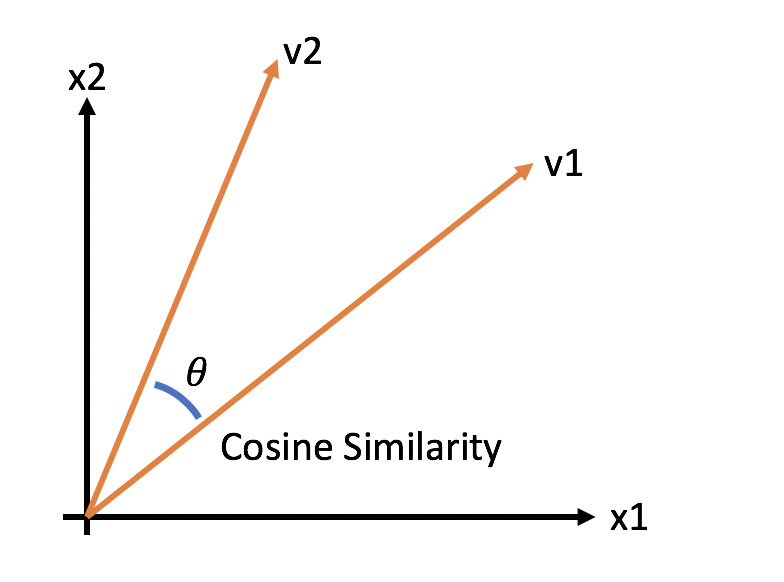
The cosine distance is used when we want to calculate the distance between two sparse vectors.
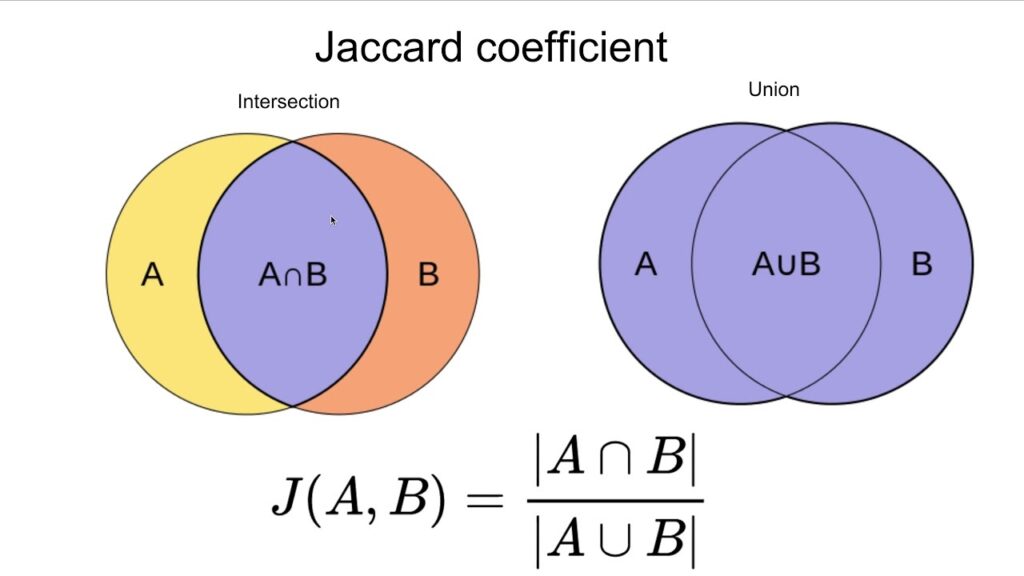
Jaccard Similarity
In Jaccard similarity is used to understand the similarity between two sample sets. The Jaccard similarity emphasizes the similarity between two finite sample sets instead of vectors and it is defined as the size of the intersection divided by the size of the union of the sample sets.
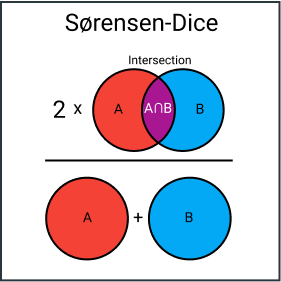
Sorensen Similarity
This measure is very similar to the Jaccard measure.
This coefficient weight matches in species composition between the two samples more heavily than mismatches. Whether or not one thinks this weighting is desirable will depend on the quality of the data. If many species are present in a community but not present in a sample from that community, it may be helpful to use Sorensen’s coefficient rather than Jaccard’s. But the Sorensen and Jaccard coefficients are very closely correlated
Haversine Similarity
It is the shortest distance over the earth’s surface – giving an ‘as-the-crow-flies’ distance between the points

